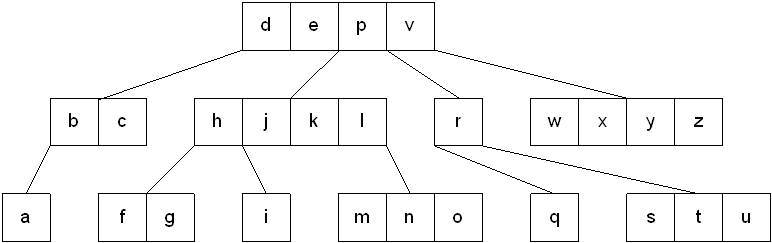
A multiway tree is a tree that can have more than two children. A multiway tree of order m (or an m-way tree) is one in which a tree can have m children.
As with the other trees that have been studied, the nodes in an m-way tree will be made up of key fields, in this case m-1 key fields, and pointers to children.
multiway tree of order 5

To make the processing of m-way trees easier some type of order will be imposed on the keys within each node, resulting in a multiway search tree of order m ( or an m-way search tree). By definition an m-way search tree is a m-way tree in which:
4-way search tree
M-way search trees give the same advantages to m-way trees that binary search trees gave to binary trees - they provide fast information retrieval and update. However, they also have the same problems that binary search trees had - they can become unbalanced, which means that the construction of the tree becomes of vital importance.
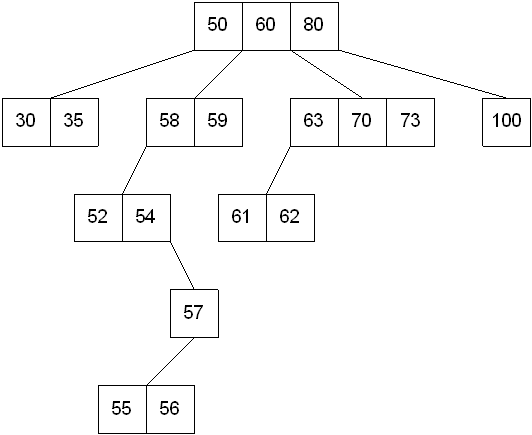
An extension of a multiway search tree of order m is a B-tree of order m. This type of tree will be used when the data to be accessed/stored is located on secondary storage devices because they allow for large amounts of data to be stored in a node.
A B-tree of order m is a multiway search tree in which:
These restrictions make B-trees always at least half full, have few levels, and remain perfectly balanced.
The nodes in a B-tree are usually implemented as a class that contains an array of m-l cells for keys, an array of m pointers to other nodes, and whatever other information is required in order to facilitate tree maintenance.
template <class T, int M>
class BTreeNode
{
public:
BTreeNode();
BTreeNode( const T & );
private:
T keys[M-1];
BTreeNode *pointers[M];
...
};
An algorithm for finding a key in B-tree is simple. Start at the root and determine which pointer to follow based on a comparison between the search value and key fields in the root node. Follow the appropriate pointer to a child node. Examine the key fields in the child node and continue to follow the appropriate pointers until the search value is found or a leaf node is reached that doesn't contain the desired search value.
The condition that all leaves must be on the same level forces a characteristic behavior of B-trees, namely that B-trees are not allowed to grow at the their leaves; instead they are forced to grow at the root.
When inserting into a B-tree, a value is inserted directly into a leaf. This leads to three common situations that can occur:
Case 1: A key is placed into a leaf that still has room
This is the easiest of the cases to solve because the value is simply inserted into the correct sorted position in the leaf node.
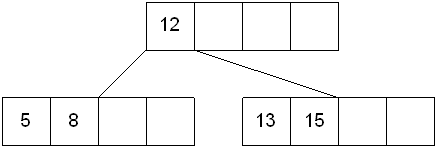
Inserting the number 7 results in:
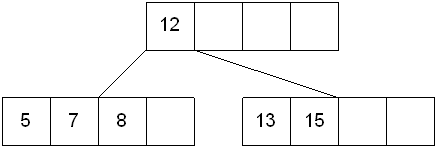
Case 2: The leaf in which a key is to be placed is full
In this case, the leaf node where the value should be inserted is split in two, resulting in a new leaf node. Half of the keys will be moved from the full leaf to the new leaf. The new leaf is then incorporated into the B-tree.
The new leaf is incorporated by moving the middle value to the parent and a pointer to the new leaf is also added to the parent. This process is continues up the tree until all of the values have "found" a location.
Insert 6 into the following B-tree:
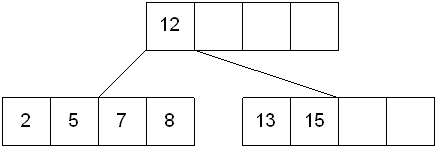
results in a split of the first leaf node:
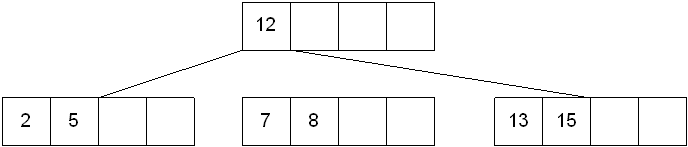
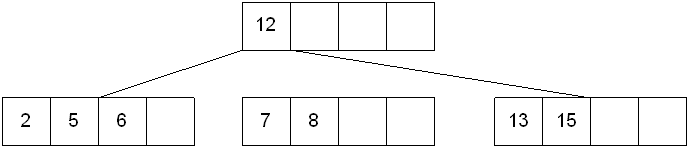
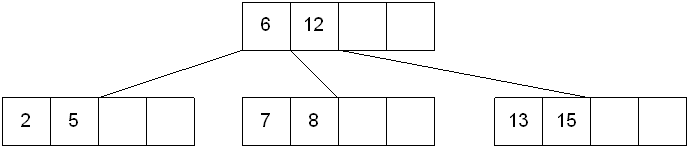
The new node needs to be incorporated into the tree - this is accomplished by taking the middle value and inserting it in the parent:
Case 3: The root of the B-tree is full
The upward movement of values from case 2 means that it's possible that a value could move up to the root of the B-tree. If the root is full, the same basic process from case 2 will be applied and a new root will be created. This type of split results in 2 new nodes being added to the B-tree.
Inserting 13 into the following tree:

Results in:

The 15 needs to be moved to the root node but it is full. This means that the root needs to be divided:

The 15 is inserted into the parent, which means that it becomes the new root node:

As usual, this is the hardest of the processes to apply. The deletion process will basically be a reversal of the insertion process - rather than splitting nodes, it's possible that nodes will be merged so that B-tree properties, namely the requirement that a node must be at least half full, can be maintained.
There are two main cases to be considered:
Case 1: Deletion from a leaf
1a) If the leaf is at least half full after deleting the desired value, the remaining larger values are moved to "fill the gap".
Deleting 6 from the following tree:

results in:

1b) If the leaf is less than half full after deleting the desired value (known as underflow), two things could happen:
Deleting 7 from the tree above results in:

1b-1) If there is a left or right sibling with the number of keys exceeding the minimum requirement, all of the keys from the leaf and sibling will be redistributed between them by moving the separator key from the parent to the leaf and moving the middle key from the node and the sibling combined to the parent.

Now delete 8 from the tree:

1b-2) If the number of keys in the sibling does not exceed the minimum requirement, then the leaf and sibling are merged by putting the keys from the leaf, the sibling, and the separator from the parent into the leaf. The sibling node is discarded and the keys in the parent are moved to "fill the gap". It's possible that this will cause the parent to underflow. If that is the case, treat the parent as a leaf and continue repeating step 1b-2 until the minimum requirement is met or the root of the tree is reached.
Special Case for 1b-2: When merging nodes, if the parent is the root with only one key, the keys from the node, the sibling, and the only key of the root are placed into a node and this will become the new root for the B-tree. Both the sibling and the old root will be discarded.


Case 2: Deletion from a non-leaf
This case can lead to problems with tree reorganization but it will be solved in a manner similar to deletion from a binary search tree.
The key to be deleted will be replaced by its immediate predecessor (or successor) and then the predecessor (or successor) will be deleted since it can only be found in a leaf node.
Deleting 16 from the tree above results in:

The "gap" is filled in with the immediate predecessor:

and then the immediate predecessor is deleted:

If the immediate successor had been chosen as the replacement:

Deleting the successor results in:

The vales in the left sibling are combined with the separator key (18) and the remaining values. They are divided between the 2 nodes:

and then the middle value is moved to the parent:
