With this algorithm, the graph is still weighted but it is now possible to have an edge with a negative weight. The addition of the negative costs causes Dijkstra's algorithm to fail because once a vertex is processed, it is never processed again. But with a negative cost, it's possible that a path back to a vertex that costs less can be found.
To fix the problem: the weighted and unweighted algorithms will be combined. This drastically increases the running time!
To do this, the vertices will no longer be marked as processed.
Pseudocode:
Push the start vertex onto a queue
Set the start vertex's distance cost to 0
while the queue is not empty
v = pop the queue
for each vertex (w) that is adjacent to v
if v's distance + edge cost between v and w is less than w's distance
w's distance = v's distance + edge cost between v and w
w's previous node = v
if w is not already in the queue
push w onto the queue
endif
endif
endfor
endwhile
Dijkstra's algorithm can be improved if the graph is known to be acyclic. The improvement is made by changing the order that the vertices are processed. It will now be done in a topological order.
This allows for the algorithm to be performed in one pass because the updating and selections can take place as the topological sort is being performed.
This works because once a vertex is selected its cost cannot be lowered since it will no longer have any incoming edges from unprocessed vertices.
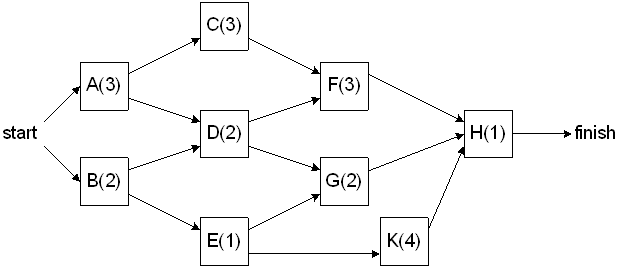
A common use for acyclic graphs is to perform critical path analysis on real world projects so that a timeline can be determined as to how long it will take to complete a project (or complete part of a project). For this type of application, each node in the graph will represent and activity that must be performed and it will include the time it takes to complete the activity. These are sometimes referred to as activity-node graphs.
The edges will represent precedence relationships. This means that if there is an edge between vertex v and vertex w, then activity v must be completed before activity w may begin.

The activity-node graph will be turned into an event-node graph when calculations are ready to be performed. This is done because it's very likely that there are some activities in the project that are dependent upon multiple activities being completed before they may begin.
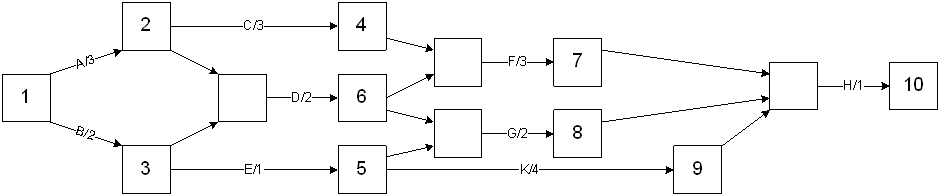
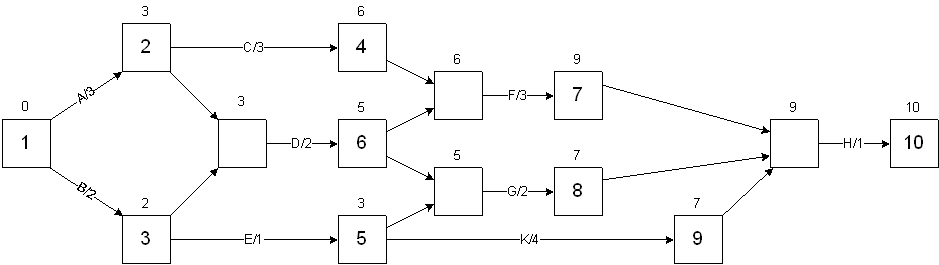
The event-node graph can then be used to find both the earliest and latest completion time for the overall project.
Earliest completion time:
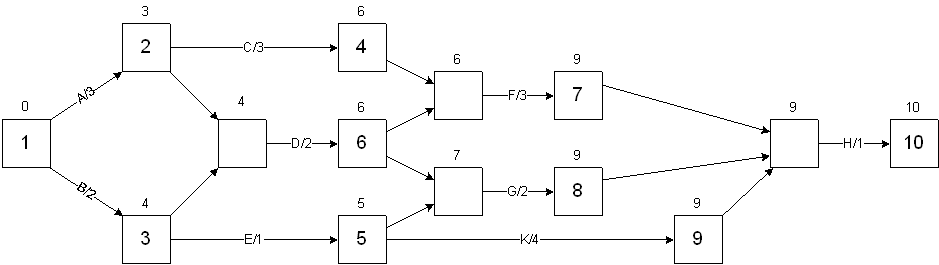
Latest completion time:
One of the basic operations that can be performed on a directed graph is a search. There are two types of searches that can be performed:
Both searches will determine which vertices are reachable from a given node.
A depth-first search of a directed graph starts from a selected vertex and then directed arcs are followed as "deeply" as possible to visit the vertices that are reachable from it that have not already been visited. Once the end of a chain is reached, backtrack to the previous node and continue the search.
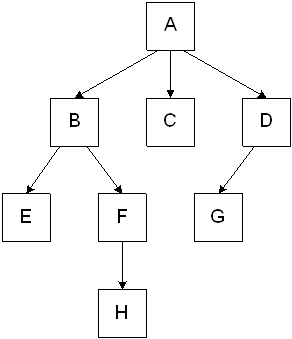
A, B, E, F, H, C, D, G
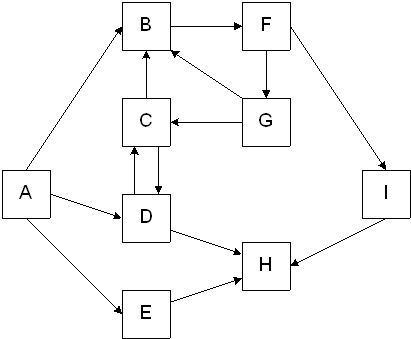
A, B, F, I, H, G, C, D, E
B, F, I, H, G, C, D
A breadth-first search of a directed graph starts from a selected vertex and then all adjacent vertices are visited. Once done, the first adjacent vertex becomes the new starting point, and all of its adjacent vertices are visited as long as they have not been previously visited.

A, B, C, D, E, F, G, H

A, B, D, E, F, C, H, G, I
B, F, G, I, H, C, D